



suivant: Effet de l'orientation des
monter: Effet de l'orientation du
précédent: Topographie du champ magnétique
Index
La figure 3.15 montre l'évolution du rapport entre la valeur
RMS du signal et la valeur RMS pour le dipôle tangentiel
en fonction de l'angle du dipôle. Pour le modèle sphérique, il est
égal à la valeur absolue du sinus de l'angle. Pour le modèle
réaliste, la valeur n'est pas nulle lorsque l'angle est égal à zéro,
mais vaut 20% de sa valeur maximale.
En fait, si l'on pose les formules dans le repère des orientations
propres du dipôle (voir section 1.2.2 pour la définition
des orientations propres), on peut écrire le moment dipolaire sous la
forme :

où  et
et  sont deux orientations propres quasi-radiale et
quasi-tangentielle, et
sont deux orientations propres quasi-radiale et
quasi-tangentielle, et  est l'angle du dipôle. Le champ magnétique
engendré est alors :
est l'angle du dipôle. Le champ magnétique
engendré est alors :
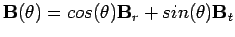
où
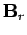 et
et
 sont les champs magnétiques
engendrés par les dipôles de même position et d'orientations
sont les champs magnétiques
engendrés par les dipôles de même position et d'orientations
 et
et  . Ils sont orthogonaux par définition.
D'où :
. Ils sont orthogonaux par définition.
D'où :

Le rapport
 permet donc de quantifier
la part de signal que le modèle sphérique ne pourra pas expliquer par
rapport au modèle réaliste. Dans cette simulation, les orientations ne
sont pas exactement des orientations propres puisque nous avons
cherché l'orientation minimisant l'amplitude maximale du signal aux
capteurs (et non le RMS) uniquement dans le plan y-z. C'est pourquoi
la courbe verte de la figure 3.15 pour le modèle réaliste
n'est pas exactement symétrique. Cependant, comme la tête est presque
symétrique par rapport au plan y-z, ces orientations ne doivent pas
être très éloignées des orientations propres. On trouve donc un
rapport de
permet donc de quantifier
la part de signal que le modèle sphérique ne pourra pas expliquer par
rapport au modèle réaliste. Dans cette simulation, les orientations ne
sont pas exactement des orientations propres puisque nous avons
cherché l'orientation minimisant l'amplitude maximale du signal aux
capteurs (et non le RMS) uniquement dans le plan y-z. C'est pourquoi
la courbe verte de la figure 3.15 pour le modèle réaliste
n'est pas exactement symétrique. Cependant, comme la tête est presque
symétrique par rapport au plan y-z, ces orientations ne doivent pas
être très éloignées des orientations propres. On trouve donc un
rapport de  pour un dipôle à une profondeur de 38 mm. Dans une
autre simulation, nous avons véritablement pris en compte les
orientations propres de dipôles situés sur un axe temporal (voir
figure 3.16). Le rapport variait entre
pour un dipôle à une profondeur de 38 mm. Dans une
autre simulation, nous avons véritablement pris en compte les
orientations propres de dipôles situés sur un axe temporal (voir
figure 3.16). Le rapport variait entre  et
et
 , avec une évolution très similaire pour les deux orientations
quasi-tangentielles. Ce rapport était plus élevé pour les dipôles
profonds.
, avec une évolution très similaire pour les deux orientations
quasi-tangentielles. Ce rapport était plus élevé pour les dipôles
profonds.
Figure 3.15:
Évolution du RMS en fonction de l'angle du dipôle : en rouge
pour le modèle sphérique et en vert pour le modèle réaliste à trois
couches. Les positions des dipôles sont représentées en vue de profil
en haut à gauche.
|
|
Figure 3.16:
Exemple d'évolution du rapport entre le RMS du dipôle quasi-radial et
les RMS des dipôles quasi-tangentiels en fonction de la position du
dipôle sur un axe temporal. Les positions du dipôle sont représentées
en vue de derrière en haut à gauche. La courbe bleue correspond au
rapport avec le dipôle quasi-tangentiel associé à la valeur propre la
plus grande et la courbe rouge au rapport avec l'autre dipôle
quasi-tangentiel.
|
|




suivant: Effet de l'orientation des
monter: Effet de l'orientation du
précédent: Topographie du champ magnétique
Index
Anne Cheylus
2002-06-25

![]() permet donc de quantifier
la part de signal que le modèle sphérique ne pourra pas expliquer par
rapport au modèle réaliste. Dans cette simulation, les orientations ne
sont pas exactement des orientations propres puisque nous avons
cherché l'orientation minimisant l'amplitude maximale du signal aux
capteurs (et non le RMS) uniquement dans le plan y-z. C'est pourquoi
la courbe verte de la figure 3.15 pour le modèle réaliste
n'est pas exactement symétrique. Cependant, comme la tête est presque
symétrique par rapport au plan y-z, ces orientations ne doivent pas
être très éloignées des orientations propres. On trouve donc un
rapport de
permet donc de quantifier
la part de signal que le modèle sphérique ne pourra pas expliquer par
rapport au modèle réaliste. Dans cette simulation, les orientations ne
sont pas exactement des orientations propres puisque nous avons
cherché l'orientation minimisant l'amplitude maximale du signal aux
capteurs (et non le RMS) uniquement dans le plan y-z. C'est pourquoi
la courbe verte de la figure 3.15 pour le modèle réaliste
n'est pas exactement symétrique. Cependant, comme la tête est presque
symétrique par rapport au plan y-z, ces orientations ne doivent pas
être très éloignées des orientations propres. On trouve donc un
rapport de ![]() pour un dipôle à une profondeur de 38 mm. Dans une
autre simulation, nous avons véritablement pris en compte les
orientations propres de dipôles situés sur un axe temporal (voir
figure 3.16). Le rapport variait entre
pour un dipôle à une profondeur de 38 mm. Dans une
autre simulation, nous avons véritablement pris en compte les
orientations propres de dipôles situés sur un axe temporal (voir
figure 3.16). Le rapport variait entre ![]() et
et
![]() , avec une évolution très similaire pour les deux orientations
quasi-tangentielles. Ce rapport était plus élevé pour les dipôles
profonds.
, avec une évolution très similaire pour les deux orientations
quasi-tangentielles. Ce rapport était plus élevé pour les dipôles
profonds.
![\begin{picture}(15,9)
\put(0,0){.}
\put(3,0){\includegraphics[height=9cm]{rms}}
...
...put(2.2,8.8){\tiny {-90{\degre}}}
\put(1.9,7.5){\tiny {0{\degre}}}
\end{picture}](img289.gif)
![\begin{picture}(14,9)
\put(0,0){.}
\put(2,0){\includegraphics[height=9cm]{raprmsvsprof}}
\put(0,7){\includegraphics[height=2cm]{posdipaxtempor}}
\end{picture}](img290.gif)