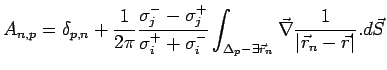Dans cette approche, les nœuds ![]() sont les centres de
gravité des
sont les centres de
gravité des ![]() triangles, notés
triangles, notés ![]() .
.

On a donc
![]() , soit, si
, soit, si
![]() et
et
![]() :
:

Les angles solides dont les centres de gravité des triangles voient
l'intérieur et l'extérieur du maillage sur lequel ils se trouvent
valent ![]() puisque la surface est régulière en ces points.
De plus, on a
puisque la surface est régulière en ces points.
De plus, on a
![]() , et l'intégrale de
surface s'annule sur tous les autres triangles que
, et l'intégrale de
surface s'annule sur tous les autres triangles que ![]() . Soit
. Soit
![]() le numéro de la surface sur laquelle
le numéro de la surface sur laquelle ![]() se trouve :
se trouve :